What Is Commutative Law Of Vector Addition
When we add two vectors we put the initial point of the second vector at the terminating point of the first vector by parallel shift. From these laws it follows that any finite sum or product is unaltered by reordering its terms or factors.
 Vector Addition Parallelogram And Triangle Laws Videos And Examples
Vector Addition Parallelogram And Triangle Laws Videos And Examples
Vector addition is commutative just like addition of real numbers.

What is commutative law of vector addition. The resultant of the vector is called composition of a vector. The commutative law of addition states that if two numbers are added then the result is equal to the addition of their interchanged position. The law states that the sum of vectors remains same irrespective of their order or grouping in which they are arranged.
This fact is known as the ASSOCIATIVE LAW OF VECTOR ADDITION. The parallelogram law or commutative law of vector addition The parallelogram demonstrates that one obtains the same vector by adding vcavcb or by adding vcbvca. A b b a.
2 See answers. What is commutative law of vector addition. Consider three vectors and.
- 33644691 vlsiddarth7 vlsiddarth7 20012021 Physics Secondary School answered What is commutative law of vector addition. If a vector is multiplied by a scalar as in then the magnitude of the resulting vector is equal to the product of p and the magnitude of and its direction is the same as if p is positive and opposite to if p is negative. If a and b are real numbers then.
Normally commutativity is taken as an axiom but you can deduce it from associativity distributivity and from the existence of inverses as follows. Let these two vectors represent two adjacent sides of a parallelogram. Therefore using the commutative property of real numbers under addition we may equivalently write.
Triangle law of vector addition is one of the vector addition laws. If you start from point P you end up at the same spot no matter which displacement a or b you take first. U v v u u v v u by distributivity u v v u by associativity u 0 u u 0 u u u 0.
The diagonal OC represents the resultant vector From ab. Vector Addition is Commutative We will find that vector addition is commutative that is a b b a This can be illustrated in the following diagram. COMMUTATIVE LAW OF VECTOR ADDITION Consider two vectors and.
The commutative property holds for both addition and multiplication but not for subtraction and division. Commutative law in mathematics either of two laws relating to number operations of addition and multiplication stated symbolically. The commutative property states that the numbers on which we operate can be moved or swapped in any position without making any difference to the answers.
Commutative Law of Addition. According to triangle law of vector addition If two sides of a triangle completely represent two vectors both in magnitude and direction taken in same order then the third side taken in opposite order represents the resultant of the two vectors both in magnitude and direction. We construct a parallelogram OACB as shown in the diagram.
12 21 3. The Mathematics law of vector addition named Parallelogram law of Addition generally states that the sum of the squares of the length of the four sides of a parallelogram is equal to the sum of the squares of the length of the two diagonals of the parallelogram. A b b a.
So u v v u. The resultant vector is known as the composition of a vector. A B A1 B1A2 B2An Bn But each component of a vector is just a real number and we know that real numbers are commutative.
This fact is referred to as the commutative law of vectr addition. There are a few conditions that are applicable for any vector addition they are. Adding these vectors under the usual rules we obtain.
Commutative Property of Addition. Vector addition is defined as the geometrical sum of two or more vectors as they do not follow regular laws of algebra. The law states that the sum of vectors remains same irrespective of their order or grouping in which they are arranged.
This fact is referred to as the commutative law of vectr addition. Then their sum is taken as the vector whose initial point is the initial point of the first and which terminates at the terminating point of the second. A b b a and ab ba.
Vector Addition is Associative. 45 54 9-36 6-3 6-3 3. The head-to-tail rule yields vector c for both a b and b a.
 Prove That Vector Addition Is Commutative Brainly In
Prove That Vector Addition Is Commutative Brainly In
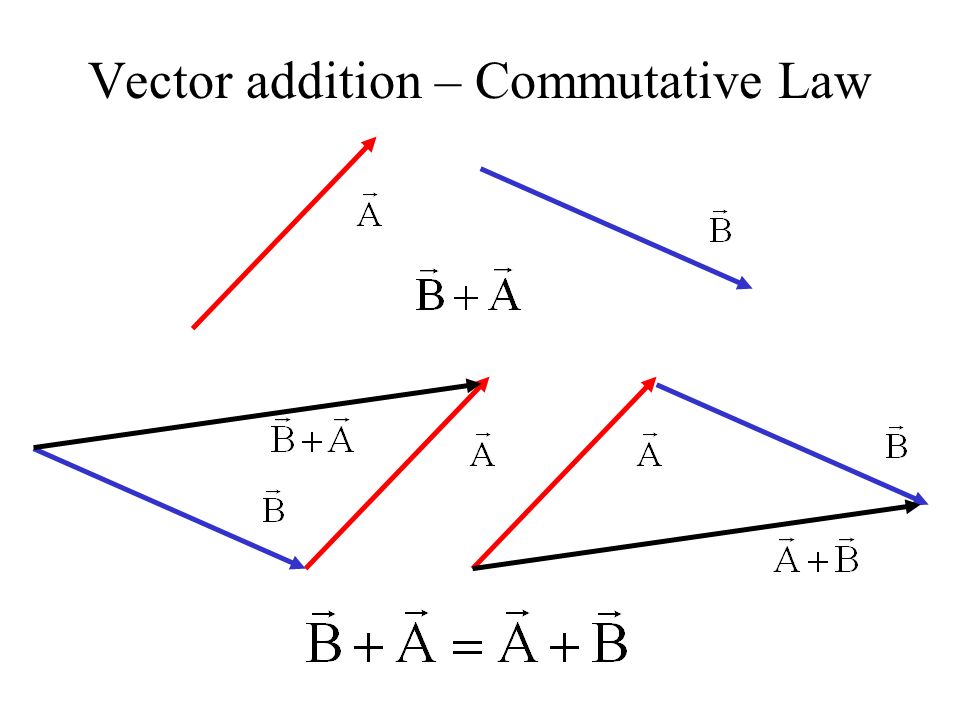 Vectors Vectors Vs Scalars Vector Addition Vector Components Ppt Video Online Download
Vectors Vectors Vs Scalars Vector Addition Vector Components Ppt Video Online Download
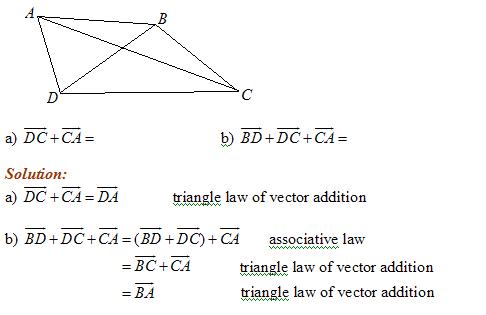 Vector Addition Solutions Examples Videos
Vector Addition Solutions Examples Videos
 Vectors Lesson 17 Commutative Law For Vectors Youtube
Vectors Lesson 17 Commutative Law For Vectors Youtube
What Are Commutative Associative And Distributive Vector Additions Quora
 State And Prove Associative Law For Vector Addition From Physics Motion In A Plane Class 11 Cbse
State And Prove Associative Law For Vector Addition From Physics Motion In A Plane Class 11 Cbse
 Associative Law Of Vector Addition Proof Youtube
Associative Law Of Vector Addition Proof Youtube
 Vector Addition Parallelogram And Triangle Laws Videos And Examples
Vector Addition Parallelogram And Triangle Laws Videos And Examples
 Vector Addition Parallelogram And Triangle Laws Videos And Examples
Vector Addition Parallelogram And Triangle Laws Videos And Examples
 Vectors Addition Is Commutative Vi If Vector U Is Multiplied By A Scalar K Then The Product Ku Is A Vector In The Same Direction As U But K Times The
Vectors Addition Is Commutative Vi If Vector U Is Multiplied By A Scalar K Then The Product Ku Is A Vector In The Same Direction As U But K Times The
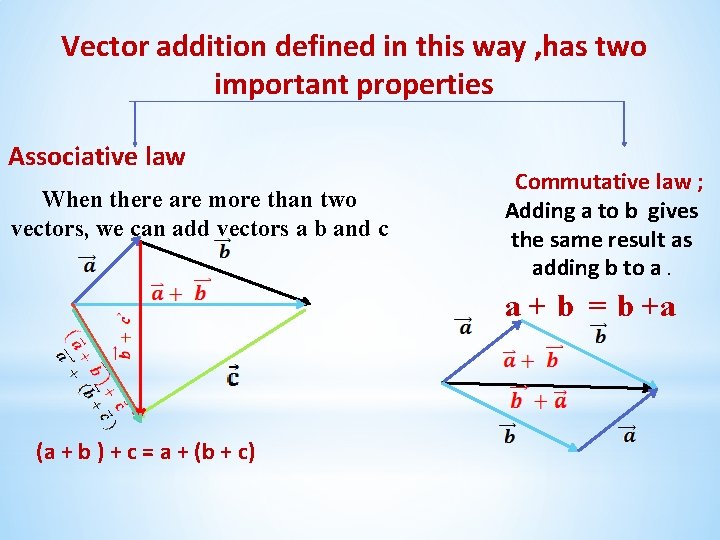 Chapter 3 V Ct Rs 3 2 Quantities
Chapter 3 V Ct Rs 3 2 Quantities
Properties Of Vector Addition Commutative Law Of Vector Addition Associative Law Of Vector Addition
 Commutative Law Of Vector Addition Youtube
Commutative Law Of Vector Addition Youtube
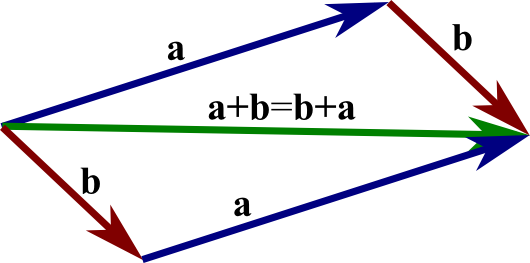 Image The Parallelogram Law Or Commutative Law Of Vector Addition Math Insight
Image The Parallelogram Law Or Commutative Law Of Vector Addition Math Insight
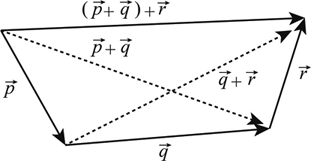 Definition Of Properties Of Vectors Chegg Com
Definition Of Properties Of Vectors Chegg Com
 State And Prove Commutative Property Of Vector Addition Physics Motion In A Straight Line 14002889 Meritnation Com
State And Prove Commutative Property Of Vector Addition Physics Motion In A Straight Line 14002889 Meritnation Com
 Properties Of Vectors Addition Youtube
Properties Of Vectors Addition Youtube
